Обработка цифровых снимков

Числовые методы обработки данных не могут полностью вытеснить визуальный.

Схема существующих числовых методов

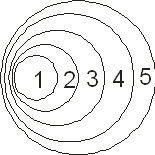
1. детерминированные подходы (строгое соответствие какому-нибудь эталону или классу)
2. Статистические модели (нестрогое соответствие)
3. Экспертные системы (более расширенный класс статистических методов) принимается при условиях неполной информации
4. Нейросетевой анализ (на базе нейронных сетей)
5. Искусственный интеллект

Визуальный метод (традиционный)

1. Основан на эвристике (от знаний человека, его квалификации)
2. Отсутствует необходимость к сложным и дорогостоящим оборудованиям
3. В основе лежит анализ яркостных характеристик, уделяется внимание косвенным признакам
4. Характерно, что человек-оператор обрабатывает одно изображение
5. Результат анализа – субъективная и качественная оценка, которая зависит от оператора и выводы всегда конкретизированы

Численный метод (современный)

1. Основан на современных достижениях в информатике, математике и других наук
2. Требуется применение современных математических методов-> возникает потребность к оборудованию->разработка ПО->специалисты
3. В основе лежит анализ яркостных и спектральных характеристик объекта +весовые характеристики
4. Анализируются данные нескольких изображений
5. Анализ является объективной и количественной оценкой

Этапы процесса обработки снимков

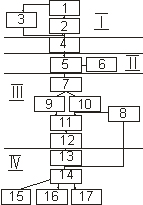
1. данные
2. Расчет статистических параметров данных
3. Предварительный просмотр снимка
4. Коррекция и восстановление снимка
5. Улучшение визуального восприятия
6. Визуальный анализ
7. Классификация изображения
8. Дополнительные данные
9. Неконтролируемая классификация
10. Контролируемая классификации
11. Классифицируемые данные
12. постобработка снимка
13. объединение данных
14. оценка точности классификации
15. карты и снимки
16. отчетные материалы
17. разнородные материалы

первый этап. Этап предварительной обработки

второй этап. Улучшение снимков (фильтрация)

третий этап. Классификация. Неконтролируемые алгоритмы IHS (интенсивность тон контраст)

PCA (анализ главных компонент ISODATA (интернациональная самоорганизующаяся методика анализа данных))

Классификации, основанные на нейронных сетях (неконтролируемые и контролируемые)

Четвертый этап. Объединение данных в ГИС.

Статистические показатели исходных данных

Рассчитаем стандартное отклонение дисперсии матрицы (ковариляционная, корялиционная). Распределение с помощью гистограммы и взаимосвязи с помощью двух или трех диаграмм рассеивания диапазона яркости. Минимальное значение диапазона яркости используется при атмосферной коррекции снимка, среднее значение является общей характеристикой распределения яркости, если среднее значение на середине шкалы, то изображение будет контрастным.

менее контрастный (темный)

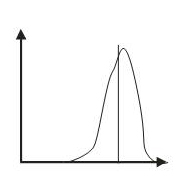более контрастный

Коряционные и ковариационные матрицы характеризуют избыточность данных. Они используются для каких-либо спектральных характеристик компонент.

Для спектрозональных снимков

	С1	С2	С3	С4
С1	С11	С12	С13	С14
С2	С21	С22	С23	С24
С3	С31	С32	С33	С34
С4	С41	С42	С43	С44

Где n – количество пикселей, – яркость пикселя к диапазону j

Коэффициент корелляции между I и j:

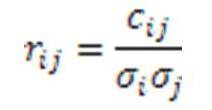
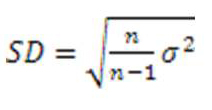
стандартное отклонение

Коэффициент корелляции – безразмерная величина в диапазоне [-1,1]

Коррекция и восстановление снимков

Эта процедура происходит до анализа.

Цель – получить максимально точное отображение действительности. У этого изображения максимальны радиометрические и геометрические характеристики.

Источники ошибок разделяют: внутренние и внешние.

Внутренние – сенсор, поэтому эти ошибки систематические.

Внешние – не систематические, возникают из-за случайных и нерегулярных изменений параметра сенсора. Для выявления этих ошибок необходимо установить связь между точками соответствующими на снимке.

Радиометрическая коррекция – это устранение ошибок, связанных с условиями съемки, устранению ошибок с состоянием атмосферы, чувствительностью сенсора, устранения, связанные с аппаратурой.

Атмосферная коррекция.

Группы:

1. Физическое моделирование (взаимодействие изменения с атмосферой) , результатом этой модели будет пересчет значений в усл.прозрачной атмосфере.

Недостаток. Нужны точные метеорологические данные и вычислительные ресурсы.

2. Метод min гистограммы . на гистограмме яркости видимого спектра выделяют наименьшее значение из всех значений всех пикселей и всех диапазонов выбирают наименьшее значение.

Недостаток. Это не точный метод.

3. Методы линейной регрессии

Данные наносят на координатную ось

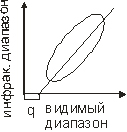
далее методом наименьших квадратов подбирают прямую, которая более подробно описывает набор данных.

Методы корректировки теплового инфракрасного излучения:

1. Метод физического моделирования (Low Trow)

2. Метод разделенного окна (яркостные температуры Tb1 Tb2 измеряются в двух, но разных близкорасположенных спектров). Яркостная температура Tb1 определяет:

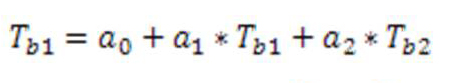
Где а1, а2, а3 – имеют разные значения для дневной и ночной поверхности, они определяются эмпирически.

Данный метод характеризуется белее точным определением температуры в пределах 0,5К. если поверхность имеет постоянную излучательную способность.

3. Двойной обзор. Точка измеряется дважды под двумя разными углами

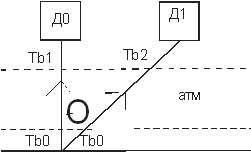
используют технику конич.съемку под углом <52⁰ надира, т.к. 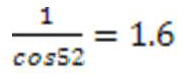, то слой атмосфера в 1,6 раза больше чем при наземной съемке. В результате двух яркостных температур можно ввести поправку.

Tb0 – изменение на исследуемой поверхности

Tb1 Tb2 – достигают датчика

Связаны уравнением переноса энергии излучения

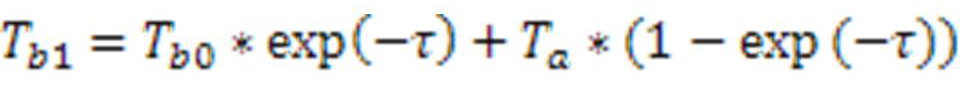
– опт. Толщина атмосферы

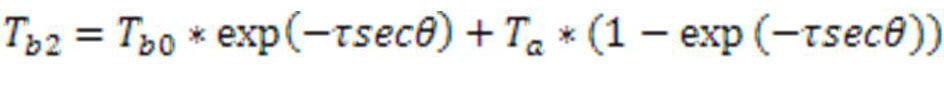
Восстановление пропущенных пикселей

Используют методы интерполяции. Также используют вычисление корреляции по известным яркостям пикселя изображения.

Геометрическая коррекция

Причины искажений:

• Ракурс съемки
• Движение сканирующей системы
• Движение спутника
• Вариации высоты, изменение ориентации спутника, скорости спутника
• Рельеф поверхности
• Вращение земли

Цель геометрической коррекции:

Устранить искажения, чтобы характеристики объекта на снимке соответствовали точнее фактическим характеристикам.

Группы:

1. Систематические. Можно учесть, смоделировав движение сенсора спутника относительно небесного тела (спутника Земли)

2. Случайные. Требуется привязка снимка в заданной системе координат для устранения ошибок.

1. Пример: 1. перекос полосы съемки. Причина – перемещение спутника кот необходимо для поворота зеркала сканирующей системы. 2. вариации скорости вращения зеркала. Приводит к изменению геометрических характеристик вдоль строк изображения. 3. панорамные искажения. Площадь сканируемой области будет пропорциональный тангенсу съемки угла (вдоль строк снимка). 4. вариации скорости платформы. Происходит последовательные проходы зеркала сканирующей системы будут соответствовать разным участкам трассы с разной длинной. 5. Вращение земли приводит к смещению вдоль строки.

2. Пример: 1. вариации высоты орбиты. 2. ориентация сканирующей системы, что одна из сканирующих систем направлена строго перпендикулярно.

Для устранения систематических ошибок необходимо знание большого число эфимеридных параметров. Для устранения случайных ошибок. Устраняют централизованные организации либо сами пользователи. Геометрическое трансформирование картографической проекции – преобразование снимка к одной из существующих картографических проекций. Для ее выполнения требуется определенное количество наземных опорных точек, для кот известны координаты этой точки на снимке. Геометрическое трансформирование применяют в том случае, если необходимо точно измерить линейные или площадные объекты. Чтобы трансформировать снимок в системе координат картограф проекции нужно выполнить 2 операции: 1. пространственная интерполяция 2. интерполяция значений яркости пикселей. Пространственная выполняется по большому числу опорных точек. В общем случае геометрическое трансформирование описывается полиномиальным преобразованием, аффинным преобразованием, для него нужно найти 6 независимым параметрам соответствовать к шести трансформациям на снимке, смещение по х,у, вращение х и у, Изменение масштаба, параллельному сдвигу границы, поворот снимка. Это фактически полином первого порядка. С математической точки зрения

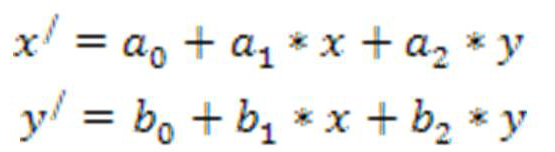(1)

Для поиска коэффициентов нам понадобятся три точки с известными координатами (х1у1)(х2у2)(х3у3)(х1\у1\)(х2\у2\)(х3\у3\)

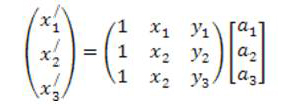
(2)

для получения коэффициентов нужно умножить каждую часть уравнения на обратную матрицу с коэффициентами

(3)

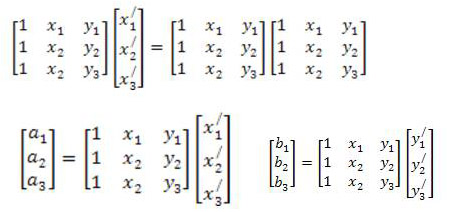
для решения данной системы должно проводить операции получения обратной матрицы и умножения матрицы. Полученные коэффициенты. подставляются в исходное уравнение и задача получения новых координат решается для каждого пикселя исходного растра. Т.о. мы получаем новую матрицу изображения, которая нам нужна. теоретически решение такой матрицы достаточно знать координаты трех опорных точек, однако на практике используют большее число опорных точек. Мы можем посчитать также среднеквадратичную ошибку

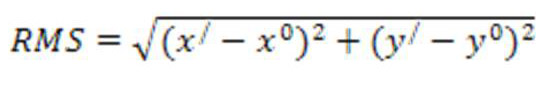
(4)

Нелинейные преобразования (полином 2-го и выше)

Корректирует нелинейные искажения. 2-го предназначены для преобразования данных географической системы координат в прямоугольные. Также используются для преобразования больших областей или для точной привязки данных, которые искажены (линзой, плохо отсканированный материал). Матрица преобразования рассчитывается также по контрольным точкам, из коэффициентов состоит. Размерность матрицы зависит от порядка используемого преобразования. Коэффициенты матрицы рассчитываются так чтобы получить формулы полиномиального преобразования как можно с меньшей ошибкой переводы исходных данных в конечную. Но получить такие коэффициенты практически невозможно.

(5)

зависимость будет апроксимироваться между ними. Количество коэф для вычисления порядка t вычисляем: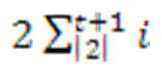

или (t+1)(t+2)(6)

Каждая контрольная точка будет влиять на расчетные коэффициенты. Если нет идеального соответствия каждой контр.точки к полиному, которые представлены расстояние между кривой и расчетной координатой точки – среднеквадратическая ошибка. Для расчета матрицы преобразования по набору контр.точек используют метод среднеквад.регрессии или метод наименьших квадратов. Формула для вычисления порядка t

(7)

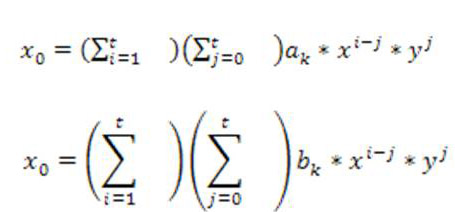
Где t – порядок полинома

Ak bk – коэффициенты

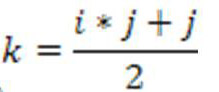
Влияние порядка преобразования

Расчет формул полинома высоких порядков у нас будет сложнее чем расчет полиномов первых порядков. Поэтому полиномы высоких порядков для привязки изображений сложных искажений. Используем одну координату – х.

(8)

полиномы выше порядка будут нелинейные. К полиному высоких порядков прибегать осторожно. Дают результаты, после которых можно не узнать изображение выходное. Преобразование высших порядков для корректировки сложных изображений ->требуется большее количество контрольных точек. Для 2-го порядка – 6 точек (парабола). Минимальное количество точек можно вычислить по формуле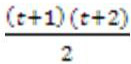

(9)

Использование меньшего количество точек на предусматривать.

Метод резинового листа (Rubber sheet)

Один из способов ортотрансформации изображения по законам нецентральной проекции. Используется при большом количестве равномерно расположенных плановых точек. Разбивают на сеть треугольников, для каждого треугольника производят трансформацию с полиномом первой степени (практически аффинное преобразование). Для каждого полученного треугольника параметры связи свои, они определяются с использованием опорных точек без контроля, использую параметры производят пересчет координат для всех пикселей внутри треугольника. Для точек на ребре пересчет производят дважды.

Интерполяция значений яркости

Интерполяция предназначена для восстановления непрерывных значений амплитуды сигнала изображения по ее дискретным значениям.

Суть – пересчет яркости пикселей старого снимка и нового – расчет дискретизации:

1. Метод ближайшего соседа

2. Метод билинейной интерполяции

3. Метод кубической свертки

1. Метод ближайшего соседа

Значения пикселя снимка определяется ближайшее значение старого снимка. Сохраняются исходные значения пикселей. Недостаток – при использовании некоторые пиксели дублируются и пропускаются. Изображение это имеет размытую структуру разрывную или блочную.

2. Метод билинейной интерполяции

Значения яркости нового пикселя B_v представляет взвешенное среднее значение интенсивности яркости ближайшего пикселя

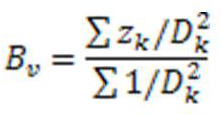
D – расстояние до пикселей старого снимка

В результате усреднения старого значения пикселей не сохраняются – недостаток.

3. Метод кубической свертки

Пиксели рассчитываются по значению 16 ближайших соседей. Старые значения пикселей не сохраняются.

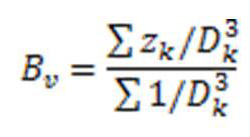
При использовании 2-х методов не будет блочной структуры

4. в плавающем окне 2*2 усреднение значения конкретного пикселя

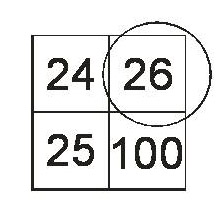
Улучшение визуального восприятия снимков

Эффект от улучшения преобразований заключается чтобы упростить дешифрирование и анализ изображения. Эта возможность появляется так как изображение в цифровом виде. Не смотря на это дешифрирование снимков может быть затруднен (вариации спектральной яркости) – не возможно выбрать оптимального диапазона яркости всех объектов.

Категории улучшения методов

1. Пространственные методы

2. Частотные методы

Пространственные методы оперируют над понятием – пространственная область (относят к плоскости изображения). Напрямую базируют над пикселями.

Частотные методы оперируют в частотной области

Функция градиентного преобразования. Значения пикселей до и после обработки: r, s.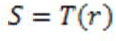

T – преобразование какое-то

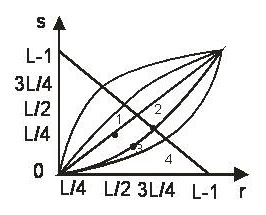
Введение в преобразование

1 линейное

-1 тождественное

2 негатив

3 n-степень

4 логарифмическое

-1 не используется

Преобразование изображения в негатив [0, L-1]. S=L-1-r. создает эквивалент фотографического негатива – для усиления белых или серых деталей.

Логарифмический. S=c*log(1+r) при r≥0

Указывает данное преобразование. Отображает узкий диапазон малых значений яркости на исходном изображении более широкий диапазон яркости в выходном изображении. Используя случай, когда необходимо использовать с проведение растяжения с современным сжатием.

Степенные преобразования

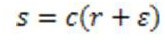
где ε- смещение

Отличие от логарифмического преобразования. Возникает семейство возможных преобразований:

Гамма-коррекция – степенное преобразование

1=1 1

2=0,62 1,5

3=0,4 2,5

4=0,2 5

5=0,1 10

6=0,04 25

Часто используемые линейные преобразования в программах обработки изображения

Повышение качества

1. Метод минимаксного растяжения. Левый и правый край гистограммы сдвигается к соответствующим границам.

2. Исключение хвостов –потенциальное преобразование