Автоматизированная обработка изображений

Компьютерная автоматизированная обработка изображений  - обработка цифровых изображений с помощью компьютера или других специальных устройств, которые построены на основе цифровых сигнальных процессорах.

Обработка – улучшение зрительно восприятия, классификация объектов, выполненная при анализе изображения.

«Эконика» - исследование общих свойств изображения, целям и задачам их преобразования методам обработки их воспроизведения и распознавания графических образов.

Цифровая передача изображений из космоса

Landsat 150 mb/s

TERRA 62 mb/s

NOAA 665 kb/s

10500, 10550 Ггц – частоты, на которых работают наши спутники

Применение – ДЗЗ, анализ местности, наблюдение за с/х угодьями, военное дело (распознавание объектов), МЧС.

Задачи:

• Улучшение качества изображения
• Измерение параметров сигналов
• Спектральный анализ многомерных сигналов
• Распознавание объектов
• Сжатие изображений

Устройства формирования изображений:

1. Электоровакумы
2. Твердотельные светочувствительные приборы

Электоровакумы имеют фотокатод, имитирующий электроны и анод на который подается положительный потенциал, действие направлено на явление внутреннего фотоэффекта. Видикон – передающая телевизионная трубка с преобразователем.

Схема видикона

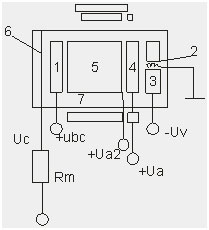
Колба (7) – фотомишень (1) и электроннооптическая система развертывания луча

Фотослой (1). При проецировании на (1) оптического изображения происходит разрядка элементарных конденсаторов прослойки мишени. При развертке лучей -> выравнивание потенциалов фотомишени. Разность потенциалов формирует сигнал изображения.

На пластину нанесен фотослой (материал, обладающий фотопроводимостью - стиблит). От толщины и свойств материала зависит чувствительность, спектральная характеристика и инерционные свойства.

Прожектор (2) состоит из оксидного подогревного катода.

Управляющий электрод (3)

Анод первый (4)

Анод второй (5)

(6) мелкоструктурная сеть обеспечивает перпендикулярный подход электронов луча по всей поверхности мишени, препятствует попаданию  ионов.

Фокусировка отклонения луча осуществляется внешней магнитной системой. Процесс формирования сигнала связано с наклонением зарядов на фотослое. Накопленный конденсатор образован пластиной, участком фотослоя. Каждый элементарный конденсатор присоединен резистором. Когда на фотомишень проецируют изображение, то величины изображения становятся разными (темные – большее освещение, светлое - меньшее). В процессе развертки, получается матрица с различным коэффициентом. Разность между токами, протекающими через резистор нагрузки, будет образовывать сигнал изображения.

Недостатки: сложные стеклянновакумные металлоконструкции ограниченный срок службы катодов и анодов мишени, очень высокое напряжение питания, ослепление, ограниченная спектральная чувствительность (до ближнего инфракрасного спектра), большая масса и габариты.

Твердотельные светочувствительные приборы обеспечивают преобразование оптических сигналов в электрические. 2 класса: тепловые, квантовые.

Квантовые основаны на изменении электрических свойств полупроводников. При поглощении фотоны передают свою энергию электрону. К ним относят фотодиоды, фоторезисторы, ПЗС. ПЗС обеспечивает более высокое разрешение, большие форматы изображения, возможность управления экспонирования, высокую однородность чувствительности элементов, меньше шума, малый вес, габариты, мощность в отличие от твердотельных. Тепловые фотоприемники изменяют электрические свойства материала при изменении его температуры. Болометрический эффект – изменение электрического сопротивления материала при нагреве вследствие изменения его температуры. Этот эффект характеризуется температурным сопротивлением материала:

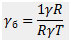
Пироэлектрические приемники. Чувствительный элемент  – фотоконденсатор. При изменении температуры изменяется диэлектрическая постоянная и емкость

Термопара. Ток меняется от «+» к «-«

При преобразовании сигнала из непрерывного  в цифровую дискретную много зависит:

• от модели,
• описывающей изображение,
• от передающей и принимающей системы,
• от каналов связи.

Модель изображения – модель функций, описывающих характеристики изображения (функция яркости, функция спектральной характеристики изображения).

Схема формирования изображения

Обработка цифровых сигналов

Изображение может быть представлено пятью элементами:

 f(x,y,z,t,λ) – функция непрерывного изображения.

Любой непрерывный сигнал S(t) может быть подвержен дискретизации по уровню t и квантованию по уровню. Если частота дискретизации сигнала F_α не меньше чем удвоенная частота  в спектре сигнала F_max: F_α≥2* F_max, то полученный дискретный сигнал будет эквивалентен S(k) согласно т.Котельникова. При помощи математических алгоритмов можно преобразовать: S(k)->S₁(k)…

Процесс преобразования сигнала – фильтрация. Виды: программная и аппаратная. Отсчеты сигналов поступают с постоянной скоростью F_α, то фильтр должен текущий отчет до поступления следующего. Чаще всего происходит, что появляются промежутки между отчетами, называется временем задержки фильтра. Для обработки сигналов фильтрации в реальном времени применяют специальные устройства – цифровые сигнальные процессоры. Этот принцип применяют для непрерывных сигналов и для сигналов, записанных на магнитные носители.

Различают методы обработки сигналов во временной и частотной области.  Эквивалентность частотно-временных сигналов определяется через преобразование Фурье. Электронный осциллограф используется во временной области. Цифровые анализаторы спектра для представления сигнала используются в частотной области.

Теорема Котельникова (Теорема отсчета).

Если аналоговый сигнал X(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, которые берутся с частотой строго больше удвоенной максимальной частоты спектра Ω, взятая с полупериодом .

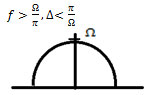
Рассмотрим для идеального случая (сигнал бесконечен, без временных разрывов). В неидеальном случае полное восстановление сигнала невозможно.

Следствие 1. Любой аналоговый сигнал может быть восстановлен, с какой угодно точностью по своим дискретным отсчетам, взятым с частотой

Следствие 2. Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый не существует.

Поэтому Теорема Котельникова утверждает, что непрерывный сигнал можно представить в виде интерполяционного сигнала:

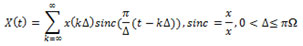
Мгновенное значение ряда и есть наши дискретные сигналы отсчета.

Восстановление сигналов, теорема отсчетов.

При дискретизации сигналов в общем случае происходит перекрытие спектров, и результирующий сигнал на произвольной частоте  представляет собой сумму многих составляющих , складывать которые необходимо с учетом их фаз.

Если учитывать лишь несколько перекрывающихся спектров, то точность может быть подвергнута сомнению. В дискр. методах частотные методы не нашли применения.

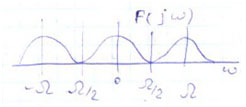
Спектр дискретизации сигнала содержит спектр исходного сигнала . В этом состоит отличие от проц-х модуляции, при которых спектр исходного сигнала отсутствует.

Исходный сигнал можно восстановить с помощью фильтрации, это только при выполнении двух  условий:

- спектры сигналов не должны перекрываться

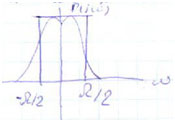
- Фильтр должен иметь идеальную прямоугольную форму, и поэтому он будет полностью пропускать  и подавлять все другие спектральные составляющие.

Первое условие требует, чтобы в спектре  не были составляющие на частотах выше , спектры не перекрываются.

Второе условие не может быть полностью выполнено, поскольку любой реальный фильтр не имеет идеальных характеристик.

Все это указывает на то, что теоретически можно идеально восстановить сигналы с ограниченным спектром по его выборка, если частота дискретизации   превышает 2x, где х – максимальная спектральная составляющая сигнала.

Представление цифровых изображений.

D(x,y), D – как правило целое число, это значение серого.

Если несколько каналов в данных, то появится несколько матриц. D(x,y,k).

Алгоритмы сжатия.

Под простым термином сжатие понимают сжатие без потерь (Lossless Compression).

Сжатие с потерями (Loss Compression) делятся на два процесса:

1)         Выделение сохраняемой части информации с помощью модели, и она зависит от цели сжатия, особенности источника и приемника информации

2)         Сжатие без потерь

Эффективность сжатия – учитывает не только степень сжатия информации (отношение длины сжатых к несжатым)  и скорость сжатия и разжатая данных.

Коэффициент сжатия  - обратная величина к степени сжатия (длина сжатых данных к несжатым).

Объем памяти, необходимый для сжатия или разжатия.

Классический алгоритм Хаффмана.

Он использует только частоту появления одинаковых байт во входном блоке данных и сопоставляет символам входного потока, который встречается чаще, цепочку битов меньшей длины, и для цепочки битов встречающихся редко – большей длины. Для сбора статистики алгоритм требует двух проходов по входному блоку. Сейчас существуют алгоритмы с одним проходом – адоптивные.

Классический алгоритм требует помещения в файл со сжатыми данными таблицы соответствия кодируемых символов и цепочек.

Характеристики алгоритма.

- степень сжатия (лучший, средний, худший);

- симметричность по времени (пропорции архивации и разархивации).

- характерные особенности: это один из алгоритмов, который не увеличивает размер исходных  данных в лучшем случае.

Арифметическое сжатие

В основе алгоритма положена идея: кодированный сигнал представляется в виде дроби, их стараемся строить таким образом, чтобы сигнал был наиболее компактным.

Эта таблица известна компрессору и декомпрессору, таким образом, кодирование будет заключаться в уменьшении рабочего интервала.

Характеристики арифметического алгоритма

-лучшая (больше 8) и худшая (1) степень сжатия;

-обеспечивает лучшую степень сжатия относительно алгоритма Хаффмана, на однотипных данных от 1 до 10% он эффективней. Также как и алгоритм Хаффмана в лучшем случае не увеличивается размер исходных данных.

Интервальное кодирование

Оно предполагает, что мы имеем дело с целыми дискретными величинами, которые принимают ограниченное число значений [0, N).

N – Число возможных значений переменных, используемых для хранения границ интервала.

Мы должны закодировать каждый символ S посредством –log₂(f_s), где f_s – частота символа s. Для каждого символа s мы можем отвести на интервале диапазон значений: [N(F_s), N(F_s+f_s))

где F_s – накопленная частота символов, предшествующих символу s в нашем алфавите,

N(f) – значение соответствующее частоте f в интервале из N возможных значений.

Чем больше будет значение N(f_s), тем точнее будет представление символа s в интервале наших значений. f_s>0. Все рассмотренные методы применимы для любой информации.

Алгоритм сжатия изображений

Основной объект – это изображение, тип данных, который характеризуется тремя особенностями:

1.Изображение требует большего объема памяти при хранении, чем текст.

2.Человеческое зрение при анализе изображения оперирует контурами, общим переходом цветов, следовательно человеческий глаз не особо чувствителен к небольшим изменениям в изображении, т.е. можно создавать архивы изображений, которые не совсем сходны со входными данными.

3.Изображение обладает избыточностью двух измерений.

Известно 3 семейства алгоритмов, разработанные только для сжатия изображений, и неприменимы для других типов данных:

1.какие критерии можно предложить для сравнений алгоритмов;

2.какие классы изображений существуют;

3.какие классы приложений существуют.

Изображение – статическое, растровое изображение, представляющее собой двумерный массив чисел, элементарная единица – пиксель.

Изображения бывают двух групп: с палитрой и без:

-у изображений с палитрой в пикселе хранится число, являющееся индексом в некотором одномерном векторе цветов – палитре, например, gif, bitmap (16,32,256);

-изображение без палитры бывает в какой-либо системе цветопредставления, например RGB, и  градациях серого (0,255).

Для того чтобы корректно оценивать степень сжатия нужно ввести понятие класса изображений. Под классом будем понимать совокупность изображений, применение к которым алгоритма архивации дает качественно одинаковые результаты.

Классы:

1. Изображения с небольшим количеством цветов (4-16) и большими областями, которые заполнены одним цветом, следовательно, плавные переходы отсутствуют;

2. Изображение с плавными переходами цветов;

3. Фотореалистичные изображения;

4. Фотореалистичные изображения с наложением деловой графики.

Классы приложений для компьютера:

1. Требовательный ко времени процедуры архивации и дизархивации;

2. Высокие требования к степени архивации и времени дизархивации;

3. Высокие требования к степени архивации.

Требования приложений к алгоритмам компрессий:

1. Высокая степень компрессии;

2. Высокое качество изображения;

3. Высокая скорость компрессии;

4. Высокая скорость декомпрессии;

5. Масштабирование изображений;

6. Устойчивость к ошибкам;

7. Требования для широковещательных сетей;

8. Учет специфики изображения;

9. Редактируемость;

10. Малая стоимость аппаратной реализации.

Критерии сравнения алгоритмов:

Характеристики алгоритмов зависят от конкретных условий, где поставлена алг степень.

-компрессия от того на каком классе алгоритмов тестировался;

-скорость алгоритмов зависит, для какой платформы разрабатывался.

1. Степень сжатия (лучшая/средняя/худшая);

2. Класс изображений, на который ориентирован алгоритм;

3. Симметричность (отношение времени кодирования к декодированию);

4. Фактор потери качества;

5. Характерные особенности алгоритма и изображений, к которым их применяют.

Рекурсивный алгоритм (wavelet) волновое сжатие

Алгоритм ориентирован на цветные и черно-белые изображения с плавными переходами. Алгоритм идеален для ч-б рентгеновских снимков. Степень сжатия от 5 до 100. При задании большего коэффициента сжатия на резких границах появляется лестничный эффект, т.е. несколько пикселей с одинаковыми яркостями.

Идея алгоритма: мы сохраняем разницу числа между средним числом соседних блоков в изображении, эти значения стремятся к 0.

Полученные значения можно округлить до целых, ещё дополнительно сжать по алгоритму Хаффмана и получить очень хорошую степень сжатия. Без потери качества можно сжимать в 4-6 раз.

Достоинство алгоритма:

- представляет возможность постепенного проявления изображения;

- упрощается показ огрубленного изображения;

- рекурсивный алгоритм в отличии от jpeg и фрактального не оперирует блоками (работает только строками).

Характеристики:

- степень сжатия от 2 до 200;

- класс изображений: предпочтительней с плавными переходами;

- коэффициент симметричности около 1,5;

- при высокой степени архивации изображение распадается на отдельные блоки.

Алгоритм jpeg2000

Отличия от стандартного jpeg:

-лучшее качество изображения при сильной степени сжатия;

-кодирование отдельных областей с лучшим качеством;

-основной алгоритм сжатия заменен на wavelet преобразования;

-для повышения степени сжатия в алгоритме используется арифметическое сжатие;

-в jpeg2000 появилась функция поддержки сжатия без потерь;

-поддержка сжатия однобитных (двухцветных) изображений.

Идея алгоритма:

Она очень похожа на обычный jpeg:

- в обоих алгоритмах используется сдвиг по яркости;

- преобразование RGB в композицию YUV, Y – яркость, UV – разница цветов.

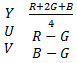
обратные преобразования: R=U+G; G=Y-[U+V/4]; B=V+G.

- дискретное wavelet преобразование;

- квантование;

- mq кодер – один из вариантов арифметического сжатия.

Общие характеристики jpeg2000

-степень сжатия от 2до 200, также имеет возможность сжатия без потерь;

-класс изображений: полноцветные 24-битные, изображения в градации без резкого перехода цветов, однобитные;

-симметричность от 1 до 1,5;

Особенности:

-позволяет удалять визуальные неприятные эффекты;

-при сильном сжатии появляется блочность и большие волны в вертикальном и горизонтальном направлении.

Обработка цифровых снимков

Числовые методы обработки данных не могут полностью вытеснить визуальный.

Схема существующих числовых методов

1. детерминированные подходы (строгое соответствие какому-нибудь эталону или классу)
2. Статистические модели (нестрогое соответствие)
3. Экспертные системы (более расширенный класс статистических методов) принимается при условиях неполной информации
4. Нейросетевой анализ (на базе нейронных сетей)
5. Искусственный интеллект

Визуальный метод (традиционный)

1. Основан на эвристике (от знаний человека, его квалификации)
2. Отсутствует необходимость к сложным и дорогостоящим оборудованиям
3. В основе лежит анализ яркостных характеристик, уделяется внимание косвенным признакам
4. Характерно, что человек-оператор обрабатывает одно изображение
5. Результат анализа – субъективная и качественная оценка, которая зависит от оператора и выводы всегда конкретизированы

Численный метод (современный)

1. Основан на современных достижениях в информатике, математике и других наук
2. Требуется применение современных математических методов-> возникает потребность к оборудованию->разработка ПО->специалисты
3. В основе лежит анализ яркостных и спектральных характеристик объекта +весовые характеристики
4. Анализируются данные нескольких изображений
5. Анализ является объективной и количественной оценкой

Этапы процесса обработки снимков

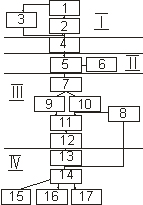
1. данные
2. Расчет статистических параметров данных
3. Предварительный просмотр снимка
4. Коррекция и восстановление снимка
5. Улучшение визуального восприятия
6. Визуальный анализ
7. Классификация изображения
8. Дополнительные данные
9. Неконтролируемая классификация
10. Контролируемая классификации
11. Классифицируемые данные
12. Постобработка снимка
13. Объединение данных
14. Оценка точности классификации
15. Карты и снимки
16. Отчетные материалы
17. Разнородные материалы

Первый этап. Этап предварительной обработки

Второй этап. Улучшение снимков (фильтрация)

Третий этап. Классификация. Неконтролируемые алгоритмы IHS (интенсивность тон контраст)

PCA (анализ главных компонент ISODATA (интернациональная самоорганизующаяся методика анализа данных))

Классификации, основанные на нейронных сетях (неконтролируемые и контролируемые)

Четвертый этап. Объединение данных в ГИС.

Статистические показатели исходных данных

Рассчитаем стандартное отклонение дисперсии матрицы (ковариляционная, корялиционная). Распределение с помощью гистограммы и взаимосвязи с помощью двух или трех диаграмм рассеивания диапазона яркости. Минимальное значение диапазона яркости используется при атмосферной коррекции снимка, среднее значение является общей характеристикой распределения яркости, если среднее значение на середине шкалы, то изображение будет контрастным.

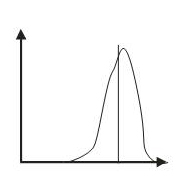
более контрастный

Коряционные и ковариационные матрицы характеризуют избыточность данных. Они используются для каких-либо спектральных характеристик компонент.

Для спектрозональных снимков

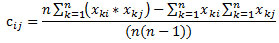
Где n – количество пикселей,  – яркость пикселя к диапазону j

Коэффициент корелляции между I и j:

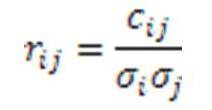
       – стандартное отклонение

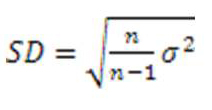  - стандартное отклонение

Коэффициент корелляции – безразмерная величина в диапазоне [-1,1]

Коррекция и восстановление снимков

Эта процедура происходит до анализа.

Цель – получить максимально точное отображение действительности. У этого изображения максимальны радиометрические и геометрические характеристики.

Источники ошибок разделяют: внутренние и внешние.

Внутренние – сенсор, поэтому эти ошибки систематические.

Внешние – не систематические, возникают из-за случайных и нерегулярных изменений параметра сенсора. Для выявления этих ошибок необходимо установить связь между точками соответствующими на снимке.

Радиометрическая коррекция – это устранение ошибок, связанных с условиями съемки, устранению ошибок с состоянием атмосферы, чувствительностью сенсора, устранения, связанные с аппаратурой.

Атмосферная коррекция.

Группы:

1. Физическое моделирование (взаимодействие изменения с атмосферой) , результатом этой модели будет пересчет значений в усл. прозрачной атмосфере.

Недостаток. Нужны точные метеорологические данные и вычислительные ресурсы.

1. Метод min гистограммы . на гистограмме яркости видимого спектра выделяют наименьшее значение из всех значений всех пикселей и всех диапазонов выбирают наименьшее значение.

Недостаток. Это не точный метод.

1. Методы линейной регрессии

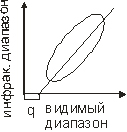
Данные наносят на координатную ось

далее методом наименьших квадратов подбирают прямую, которая более подробно описывает набор данных.

Методы корректировки теплового инфракрасного излучения:

1. Метод физического моделирования (Low Trow)
2. Метод разделенного окна (яркостные температуры Tb1 Tb2 измеряются в двух, но разных близкорасположенных спектров). Яркостная температура Tb1 определяет:

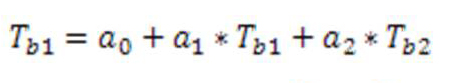
Где а1, а2, а3 – имеют разные значения для дневной и ночной поверхности, они  определяются эмпирически.

Данный метод характеризуется белее точным определением температуры в пределах 0,5К. если поверхность имеет постоянную излучательную способность.

3. Двойной обзор.

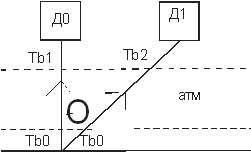
Точка измеряется дважды под двумя разными углами используют технику конич. съемку под углом <52⁰ надира, т.к. , то слой атмосфера в 1,6 раза больше чем при наземной съемке. В результате двух яркостных температур можно ввести поправку.

Tb0 – изменение на исследуемой поверхности

Tb1 Tb2 – достигают датчика

Связаны уравнением переноса энергии излучения

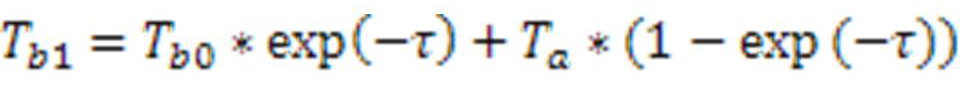
 – опт. Толщина атмосферы

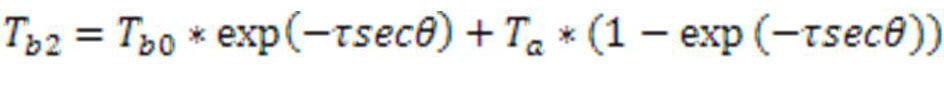
Восстановление пропущенных пикселей

Используют методы интерполяции. Также используют вычисление корреляции по известным яркостям пикселя изображения.

Геометрическая коррекция

Причины искажений:

• Ракурс съемки
• Движение сканирующей системы
• Движение спутника
• Вариации высоты, изменение ориентации спутника, скорости спутника
• Рельеф поверхности
• Вращение земли

Цель геометрической коррекции:

Устранить искажения, чтобы характеристики объекта на снимке соответствовали точнее фактическим характеристикам.

Группы:

1. Систематические. Можно учесть, смоделировав движение сенсора спутника относительно небесного тела (спутника Земли)

2. Случайные. Требуется привязка снимка в заданной системе координат для устранения ошибок.

1. Пример: 1. перекос полосы съемки. Причина – перемещение спутника кот необходимо для поворота зеркала сканирующей системы. 2. вариации скорости вращения зеркала. Приводит к изменению геометрических характеристик вдоль строк изображения. 3. панорамные искажения. Площадь сканируемой области будет пропорциональный тангенсу съемки угла (вдоль строк снимка). 4. вариации скорости платформы. Происходит, последовательные проходы зеркала сканирующей системы будут соответствовать разным участкам трассы с разной длинной. 5. Вращение земли приводит к смещению вдоль строки. 

2. Пример: 1. вариации высоты орбиты. 2. ориентация сканирующей системы, что одна из сканирующих систем направлена строго перпендикулярно.

Для устранения систематических ошибок необходимо знание большого число эфимеридных параметров. Для устранения случайных ошибок. Устраняют централизованные организации либо сами пользователи. Геометрическое трансформирование картографической проекции – преобразование снимка к одной из существующих картографических проекций. Для ее выполнения требуется определенное количество наземных опорных точек, для кот известны координаты этой точки на снимке. Геометрическое трансформирование применяют в том случае, если необходимо точно измерить линейные или площадные объекты. Чтобы трансформировать снимок в системе координат картограф проекции нужно выполнить 2 операции: 1. пространственная интерполяция 2. интерполяция значений яркости пикселей. Пространственная выполняется по большому числу опорных точек. В общем случае геометрическое трансформирование описывается полиномиальным преобразованием, аффинным преобразованием, для него нужно найти 6 независимым параметрам соответствовать к шести трансформациям на снимке, смещение по х,у, вращение х и у, Изменение масштаба, параллельному сдвигу границы, поворот снимка. Это фактически полином первого порядка. С математической точки зрения

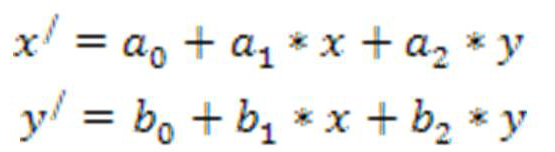
Для поиска коэффициентов нам понадобятся три точки с известными координатами (х1у1)(х2у2)(х3у3)(х1\у1\)(х2\у2\)(х3\у3\)

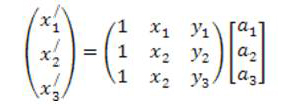
для получения коэффициентов нужно умножить каждую часть уравнения на обратную матрицу с коэффициентами

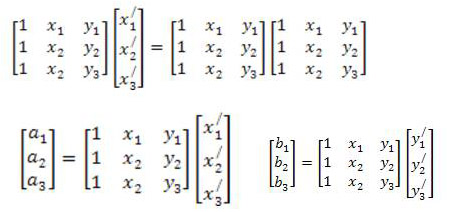
для решения данной системы должно проводить операции получения обратной матрицы и умножения матрицы. Полученные коэффициенты. подставляются в исходное уравнение и задача получения новых координат решается для каждого пикселя исходного растра. Т.о. мы получаем новую матрицу изображения, которая нам нужна. теоретически решение такой матрицы достаточно знать координаты трех опорных точек, однако на практике используют большее число опорных точек. Мы можем посчитать также среднеквадратичную ошибку

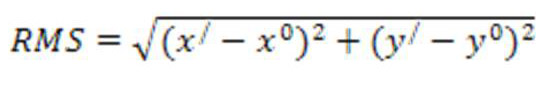
Нелинейные преобразования (полином 2-го и выше)

Корректирует нелинейные искажения. 2-го предназначены для преобразования данных географической системы координат в прямоугольные. Также используются для преобразования больших областей или для точной привязки данных, которые искажены (линзой, плохо отсканированный материал). Матрица преобразования рассчитывается также по контрольным точкам, из коэффициентов состоит. Размерность матрицы зависит от порядка используемого преобразования. Коэффициенты матрицы рассчитываются так чтобы получить формулы полиномиального преобразования как можно с меньшей ошибкой переводы исходных данных в конечную. Но получить такие коэффициенты практически невозможно.

зависимость будет апроксимироваться между ними. Количество коэф для вычисления порядка t вычисляем:

 или (t+1)(t+2)

Каждая контрольная точка будет влиять на расчетные коэффициенты. Если нет идеального соответствия каждой контр. точки к полиному, которые представлены расстояние между кривой и расчетной координатой точки – среднеквадратическая ошибка. Для расчета матрицы преобразования по набору контр. точек используют метод среднеквад. регрессии или метод наименьших квадратов. Формула для вычисления порядка t

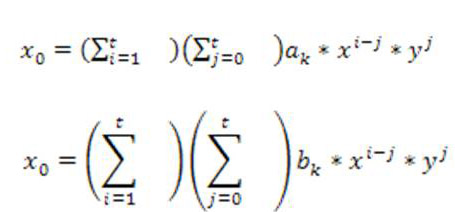
Влияние порядка преобразования

Расчет формул полинома высоких порядков у нас будет сложнее, чем расчет полиномов первых порядков. Поэтому полиномы высоких порядков для привязки изображений сложных искажений. Используем одну координату – х.

полиномы выше порядка будут нелинейные. К полиному высоких порядков прибегать осторожно. Дают результаты, после которых можно не узнать изображение выходное. Преобразование высших порядков для корректировки сложных изображений ->требуется большее количество контрольных точек. Для 2-го порядка – 6 точек (парабола). Минимальное количество точек можно вычислить по формуле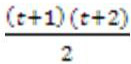 

Использование меньшего количество точек на предусматривать.

Метод резинового листа (Rubber sheet)

Один из способов ортотрансформации изображения по законам нецентральной проекции. Используется при большом количестве равномерно расположенных плановых точек. Разбивают на сеть треугольников, для каждого треугольника производят трансформацию с полиномом первой степени (практически аффинное преобразование). Для каждого полученного треугольника параметры связи свои, они определяются с использованием опорных точек без ко